Papers


5) Backscattering
So far we have considered the CW and CCW oscillations to be independent of each other.This is largely accurate, except for the effect of backscattering, when the light from one wave is scattered back into the other wave. Despite best efforts in polishing the optical surfaces, there is always some scattering, which you can readily see by looking at the mirrors. Scattering is generally isotropic, but a very small fraction of the light is directed backwards, resulting in the coupling of the two modes. The exact treatment of backscattering is rather complicated, but it can be qualitatively understood by assuming that the reflection coefficient of the mirrors has a small imaginary component to account for the phase of the light scattered backward. As a result, the laser frequency does not need to perfectly satisfy the relationshipν = nc / L , a small phase shift of the electric field wave is now possible after a complete pass, resulting in a slightly different oscillation frequency. For a very small rotation rate, the frequencies of CW and CCW waves can become identical with a constant phase relationship between the two waves resulting in a higher overall gain due to their constructive interference. The two waves can thus become locked to each other at low rotation rates. At sufficiently large rotation rate the phase mismatch in the cavity can no longer be balanced by light scattering and the beat frequency between CW and CCW modes returns to the expected value for the Sagnac effect. The beat frequency corresponding to the onset of back-scattering lock can be estimated as νL~ bc/L, where b is the backscattering coefficient. Backscattering frequency lock is a serious problem for laser gyroscopes since most practical measurements are performed near zero rotation rates. One usually introduces a dithering mechanism that artificially induces a frequency difference between CW and CCW modes, not allowing them to come close to each other in frequency.

6) Transverse profile of cavity light
One can analyze the transverse profile of the standing wave in the cavity quantitatively with a widely used ABCD-matrix technique for calculating the propagation of light through multiple mirrors, lenses and other optical elements. A light ray at a certain position z along the optic axis is described by two numbers: the distance from the optic axis r and its slope r'=dr/dz. The transformation of the ray by optical elements is given by
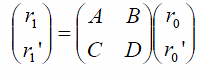
One can easily derive the “ABCD” matrix for simple cases:
Empty space of length d:
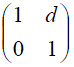
Thin lens with focal distance f:
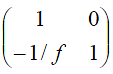
Mirror with radius of curvature R:
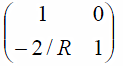
If the mirror axis is tilted relative to the optic axis by an angle θ, the effective radius of curvature is Re=Rcosθ in the tilt direction and Re=R/cosθ in the orthogonal direction. For multiple elements the ABCD matrices are simply multiplied together. For example, consider a ray at a distance x from the optic axis initially propagating parallel to the axis, going through a lens of focal distance f and then empty space of length f. At that point it will have coordinates:
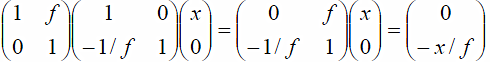
Hence, the ray will pass through the optic axis with a slope r'=−x/f, as expected. Arbitrary complicated optical systems can be modeled this way. ABCD law works in the “paraxial” approximation when r' = tan(r') = sin(r') and does not include the effects of spherical aberration. However, these effects are usually quite small in an optical cavity. The effects of diffraction in the cavity can be easily combined with the ABCD matrix technique for Gaussian beams. Without going through detailed derivation, we write the electric field as
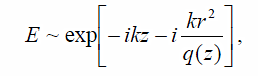
where k is the light wavevector, z is the distance in the direction of propagation of the light and r is the distance away from the beam center. Hence the transverse intensity profile of the light beam, given by EE*, is a Gaussian with a width given by the imaginary part of 1/q(z). It turns out that the shape of a Gaussian laser beam after propagating through an optical system is given by
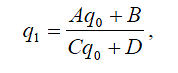
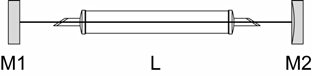
where q0 is the inital value of the q parameter and q1 is its value at the output of the system described by the ABCD matrix. Hence, when given an initial value of q one can determine the shape of the Gaussian beam as it propagates through an arbitrary optical system. In a cavity the laser beam has to retrace itself after one complete pass. Hence, we need q1 = q0 when the ABCD matrix represents all elements in the cavity (including empty space). The solution of this equation (if it exists) gives the transverse shape of the standing wave in the cavity. If there is no solution, there will be no stable standing waves in the cavity. In our case, the two mirrors near the laser tube have a radius of curvature of 2 meters and the output coupler is flat. One can calculate the profile of the standing wave (separately in the horizontal and the vertical plane) by constructing the ABCD matrix for the cavity.
7) Experimental Procedure
1. Remove the etalon from the cavity. Turn on the power supply for the laser tube and wait a few seconds until the electrical discharge starts. If the laser oscillations start immediately, which you can see by a bright spot on the mirrors, you can proceed to step 3.
2. If the oscillations do not start, the mirrors are slightly misaligned. Usually the oscillations can be reestablished by small adjustments of the mirrors, but one has to be very careful. A gross misalignment of the mirrors will require a time-consuming total laser realignment. On one of the cavity mirrors make very small adjustments to one of the tilt knobs. Rotate the knob by just a degree or so. If you don’t see laser light, try the other tilt knob. If that doesn’t work, systematically rotate one tilt knob by small steps while scanning the other knob by ±5 degrees around its initial position. Keep track of which direction you are scanning the mirror and
reverse it if necessary, until you see a flash of laser light. Never make adjustments to more than one mirror at a time. Using this procedure you can usually get the laser to oscillate. If it doesn’t work, go to the gross laser realignment procedure described at the end of the document.
3. With the laser oscillating, take a small piece of paper and trace all laser beams coming out of the cavity. Follow the path of CW and CCW beams. Place the power meter in the path of one of the beams coming out of the output coupler. Maximize the laser power by making small adjustments to the cavity mirrors. Now you can make adjustments to all mirrors, but go in small steps so you don’t loose the oscillations. If you see excessive scattering of light from the mirror surfaces, you can clean them using tissue paper and methanol. Fold the tissue paper many times and put a few drops of the methanol on it, swipe wet tissue paper across the surface of the mirror in only one direction. Do not re-use the tissue paper and do not touch or rub the mirror surfaces!
4. With the power meter, measure the intensity of all beams coming out of the cavity, not onlyfrom the output coupler, but also from other mirrors.
5. Measure the reflectivity of all the mirrors. For this purpose you can use an auxiliary HeNe laser that is provided. Place the laser so its beam is approximately parallel to the beam circulating in the cavity and measure the power before and after the mirrors.
6. Trace the laser beams coming out of the cavity for some distance, until they expand to several millimeters in size. With the camera provided, take pictures of the laser spots. Be careful to adjust camera settings so the spot is not saturated. Measure the distance to the plane of the picture and use the ruler or ruled paper to find the scale of your photograph. Also measure the distances between all mirrors (do not touch the mirror surfaces!).
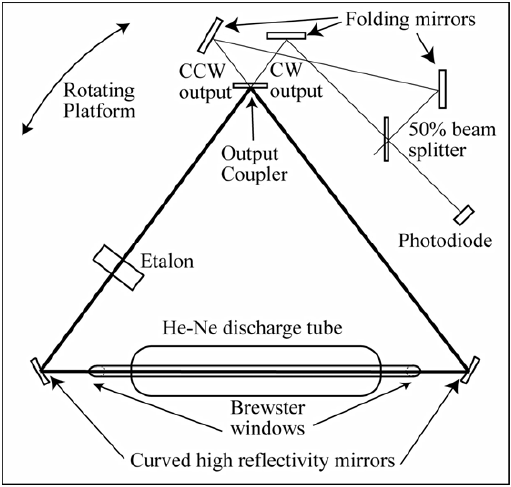
7. Trace the CW and CCW beams coming out of the output coupler. They are combined on a 50% beamsplitter. Remove the photodiode and follow the paths of the beams. They should be well overlapping over a large distance. Place the photodiode back and look at the signal on the oscilloscope as you rotate the cavity. You should clearly see oscillations in the photodiode signal for relatively fast rotations due to beating of CW and CCW waves, but they may vanish for slow rotations due to backscattering lock.
8. To rotate the experiment at a uniform speed you can use the electrical motor, slide the rotating shaft under the breadboard. You need to manually reverse the direction of the motion when it runs out of range and measure the speed of rotation using a stop watch.
9. Record the photodiode output for several rotation speeds of the breadboard in both directions to determine its frequency. Determine approximately the frequency at which the lock-in occurs.
10. Insert the etalon into the laser. There are many possible tilt angles of the etalon that will result in laser oscillations. Make small adjustments until you find one that makes the laser oscillate. Find the reflection from the etalon on one of the mirrors. You can make adjustments to both etalon angles to find a ring of possible etalon reflections.
11. Rotate the experiment at different speeds and observe the behavior of the photodiode output. Compare the contrast of the beat oscillations and the scattering lock range to the case of no etalon.
8) Analysis
1. From measurements of the reflectivity of the mirrors, estimate the round-trip loss of the cavity (which is balanced by the gain when the laser is operating). Calculate the power of the light circulating in the cavity during operation.
2. Calculate the Gaussian parameter q in the cavity and the expected size of the laser beam as it exits the cavity. Compare with your photographs of the light profile. You can use free image analysis software, such as ImageJ, to extract the transverse intensity profiles from your photographs.
3. Determine the gyroscope beat frequency as a function of the rotation rate. Compare it to the predicted scale factor from the geometrical size of the laser cavity.
4. Compare the behavior of the cavity with and without the etalon. Work out the math of the beating between the CW and CCW waves in the photodiode, consider what happens when there are multiple laser frequencies. Comment on the longitudinal mode structure of the laser and the effect of the backscatter in the presence of the etalon.
9) Gross laser realignment procedure
If you cannot establish laser oscillations after careful small adjustments of one of the mirrors, you might need to realign the laser from scratch. This is a time-consuming procedure to be avoided if possible. Turn on the auxiliary HeNe laser and send it into the cavity through the output coupler. There is an extra mirror provided to help with alignment of the HeNe laser. The HeNe laser beam should
go through the center of the output coupler and hit the center of one of the curved mirrors. Make sure the etalon is out of the cavity.
The reflection from the curved mirror has to go through the discharge tube and hit the other curved mirror. If it doesn’t, remove the discharge tube from the path of the laser by unscrewing the screws holding it to the optical breadboard. Adjust the first curved mirror until the laser hits the center of the second curved mirror Place back the discharge tube into the path of the beam. Adjust its height and position until the laser goes cleanly through the center of the tube and comes out undistorted. Now steer the second curved mirror so the laser beam hits the center of the output coupler. It should hit the exact spot where the HeNe beam first comes into the cavity. Finally, adjust the tilt of the output coupler, so the reflection of the beam that made one complete run around the cavity
is directed to the center of the first curved mirror. Now the mirrors are roughly adjusted to allow a laser beam to go around the cavity and through the discharge tube. If you turn off the light, you should see multiple reflections on the mirrors. The goal is to make all the reflections overlap. This is not trivial, as there is now coupling between all the mirrors. Make small adjustments to the tilt of the cavity mirrors to allow as many reflections to go around the cavity as possible. If the discharge tube is on, you should see a flash of light from the laser. Make small adjustments to the mirrors until it appears. If you don’t see anything, make sure the path of the external laser beam does not hit any scratches on the mirrors or other places that cause excessive scattering. References Laser Gyro Experiment, Dr. Klaus Dickmann, Dept. Engineering Physics Münster University of Applied Sciences, Germany. – source for some of the figures in the write-up J. R. Wilkinson, Ring Lasers, Progress Quanum. Electronics. 11, pp. 1-103, (1)
© FOGphotonics, inc. | Company | Products | Technoloy | Contact us






